I recently completed a University course for teachers titled, Integration of Information and Computer Technology, where the focus is on improving the teaching and learning process through technology-driven learning. I thought I was signing up for a routine online learning experience, where I may have struggled to find the time needed to complete the assigned modules. I did not expect to become so engaged and excited about all of my learning experiences! By signing up for this online course, I met Brian Aspinall who inspired me to learn how to code, and to use coding to empower students in their learning journey. 

The final project for this online course was the creation of three lesson plans, in three-part design format, centered on the use of technology in the teaching and learning process. I will share with you my detailed lessons, along with all resources including the two games I created in Scratch, which are geared towards students in the Grade 12 Mathematics of Data Management course, as outlined in the Ontario Curriculum. However, any educator of intermediate to senior level math who is looking for an engaging way to teach probability concepts may find the ideas and/or resources in these lessons useful. I strived to create lessons where: students use code to bring the concepts of probability to life; students have voice and choice; students collaborate with each other to create their own meaning; students have fun playing with math! 

Before you dive into these lessons, I’d like to give you some background information on how I became so inspired to teach through code. In his books, Code Breaker and Block Breaker, Brian clearly conveys that relationships are at the heart of learning. 

“The real 1:1 is more about personal connections we make with every student and less about the number of devices our classrooms have. #BlockBreaker” (p.69). 

“We need to stop trying to make kids conform to our world and, instead, embrace theirs.  #CodeBreaker” (p.24).

“You do not inspire people by showing them how powerful you are. You inspire people by showing them how powerful they are. -Alexander Den Heijer.  #BlockBreaker” (p.18).

“When student work is seen as fixable, rather than right or wrong, we imply growth. This mindset challenges us to redefine what it means to fail at school. #BlockBreaker” (p. 20).

To be honest, I was not expecting to read so many ideas that resonated with my own vision of education – one where students are at the centre of learning; where teachers meet students at their level and design effective, engaging, relevant learning experiences for all students to create their own meaning. 

Reading Brian’s books has also refined my understanding of what coding and computational thinking (CT) actually look like in the classroom. CT is a thinking process where individuals use logical reasoning to break down a problem or challenge into small manageable steps; recognize patterns; focus on relevant information; create step-by-step solutions to solve problems. Coding is a final step in the CT process (Block Breaker, p. 33).

It is very interesting to learn that Brian’s books are about “breaking” out of the status quo. Brian clearly describes how so many students feel about learning in traditional math classrooms: boring! Brian discusses that the question isn’t whether we use technology today, but how we use it. Instead of focusing on technology, or specific tools, Brian challenges his readers to focus on our pedagogy. We need to ask ourselves what we want our students to truly learn from the experiences we create in our classrooms? As a secondary math teacher for over 12 years, reading Brian’s books have inspired me to try something that I haven’t done before in teaching – coding in the math classroom.  My new knowledge has given me the tools to better align my instructional practices with the vision of my school, which is home to a Science and Technology regional program. 

In Code Breaker, Brian clearly describes how he has used coding in his classes, including his math classes. I enjoyed taking a peak into his classroom to see just how coding and computational thinking is applied from his standpoint. There are many examples that I can personally relate to, such as the coin-flipping activity in the experimental vs. theoretical probability lesson that Brian gave to his own students. I was literally laughing out loud when I read the part about the classroom turning into a noisy jungle with change flying all over the classroom. That’s exactly what happened with my own students! Was the lesson fun, especially for a math class? Sure. Were the students truly engaged and thinking about the concepts at hand? Probably not. I appreciate how down-to-earth Brian is in conveying his teaching experiences, and the “aha” moments he had throughout his own teaching journey. Brian writes that a student approached him and asked if he could code a flip-coin simulator. Through this experience, the student became highly engaged with an otherwise routine math assignment. Creating the coin-flipping simulator became his “passion” project. To me, this example portrays just how powerful learning can be when students are allowed to create their own meaning through relevant activities, without the constraint of time. It also shows how powerful learning can be when teachers allow students the space needed to learn using their preferred strategies, and not what is provided by the teacher.

After reading about the issue of time constraint in schools, I was reminded of the fact that teaching and learning should be about focused on the process of learning, and not on the outcome – which, at the secondary level, is usually a paper and pencil test that does not help the student learn and grow the way authentic assessment is intended. Then I remembered my own experiences as student who majored in Pure Mathematics. To this day, I can still vividly remember how petrified I felt on math exams, even when I was more than prepared to write the tests. Through these experiences, I was even more determined as an educator to design effective instructional and assessment strategies that help students learn and grow, and gain a deep conceptual understanding of concepts, instead of becoming stressed out over meaningless performance-based tasks.

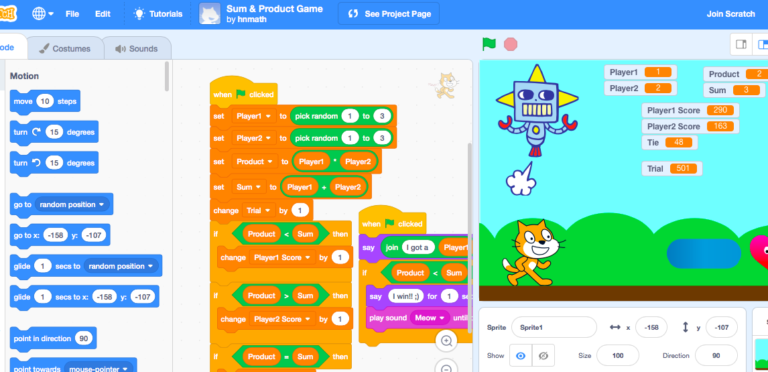
Armed with this frame of mind, I set out to empower students through voice and choice and to bring the beauty of mathematics to life through coding! In the first two lessons, students are introduced to basic probability concepts through The Sum & Product Game I created in Scratch, which is based on an investigation found in the Mathematics of Data Management textbook by McGraw-Hill Ryerson (2002), p. 304. Check out The Sum & Product Game here.  

The Sum & Product Game details: when the green flag is clicked player 1 (the cat) and player 2 (the robot) will generate a random number between 1 and 3. 

Rules of the game: 

1. If the product < sum, player 1 gets a point. 

2. If the product > sum, player 2 gets a point. 

3. If the product = sum, no one gets a point. 

By pressing the Turbo button, students can set the number of trials, to 20, 50, 100, 1000, etc., and notice the scores of each player. Some questions to think about: Does one player have an advantage over the other? How do you know? How many outcomes are there in this game? This game can be used to introduce basic probability concepts and define a probability experiment: a well-defined process consisting of a number of trials, with clearly defined outcomes, sample space, and events.

In the third lesson, I focus on experimental vs. theoretical probability and use the Three-Coin Toss Game I created in Scratch to uncover the idea that as the number of trials increases, experimental probabilities approach theoretical probabilities. The Three-Coin Toss game can be found here. In this game, we analyze how many heads come up when three coins are tossed: 0 heads, 1 head, 2 heads, or 3 heads. Using the turbo feature, we see that the experimental probability of tossing 0H, 1H, 2H and 3H approaches the theoretical probabilities for each event. This game is modelled from an investigation in the Data Management 12 (2014) textbook by McGraw-Hill Ryerson (p.26). 

The detailed lesson plans, along with all resources, can be found here.

Please feel free to use any ideas and/or resources the way you see fit. If you get a chance to use any of these lessons in the new school year, I’d love to hear from you. You can connect with me on Twitter @MsNizam5. 

To see some other ways that I have engaged students in the math classroom, you can check out my interview with the Toronto Star where I discuss the creation of the music video projects with my Calculus and Vectors students. As a result of this engaging activity, my Calculus students nominated me for the Toronto Star teacher award in 2014. I was given an honourable mention by the Toronto Star.  The exciting teaching and learning journey of creating the music videos is a time in my career that I will never forget!

If you are interested in using math to help your students learn about social justice and equity issues, you can take a look at the MCV 4U0 Process Folio. This project is a collection of activities for Calculus and Vectors students, centered on using the tools of calculus to understand issues of social justice, with a focus on the 7 mathematical processes. I was one of the lead writers in this project, developed in 2012, and created the activities and resources for the first chapter, rates of change.

My name is Hudaser Nizam and I have been teaching secondary level mathematics for 13 years in Brampton, Ontario, Canada for the Peel District School Board. For the past nine years I have also been the curricular head of mathematics. I graduated from York University, Toronto, Ontario, in 2006 with a major in Pure Mathematics, a minor in Economics, and earned my B.Ed. in the Concurrent Education program. I am married and raising two energetic boys, aged 8 and 2 years old. I am passionate about learning new things, I love music and playing the piano, and I enjoy reading in my spare time. I earned my Master of Education degree from the University of Toronto in 2011, where I studied Educational Administration with a focus in social justice and equity issues. I had the opportunity to teach an AQ course for educators who wish to teach mathematics at the intermediate level. In 2012, I was one of the lead authors in a writing project for my school board where a group of educators created hands-on activities and lessons for the Calculus and Vectors course. This project was designed to help students understand social justice and equity issues in Canada using the tools of Calculus. In 2014 I was nominated by my Calculus students for the Teacher Award given by our newspaper, The Toronto Star, for making Calculus engaging through the use of our music video project. I was given an honourable mention by the Toronto Star. I believe all students can learn mathematics and I do whatever it takes to help each student reach their highest potential. I strive to make math learning fun, relevant and connected to students’ lives.