In this post I would like to provide a lesson based on patterning, spatial awareness and computational thinking using Minecraft.

From the Ontario curriculum for grade 8:

• determine a term, given its term number, in a linear pattern that is represented by a graph or an algebraic equation;
• make connections between solving equations and determining the term number in a pattern, using the general term (e.g., for the pattern with the general term 2 n + 1, solving the equation 2 n + 1 = 17 tells you the term number when the term is 17);
• solve and verify linear equations involving a one-variable term and having solutions that are integers, by using inspection, guess and check, and a “balance” model (Sample problem:What is the value of the variable in the equation 30x – 5 = 10?).

I also like to mention the 6 Cs as they fit our board’s engagement model:

Character Education— honesty, self-regulation and responsibility, perseverance, empathy for contributing to the safety and benefit of others, self-confidence, personal health and well-being, career and life skills.

Citizenship — global knowledge, sensitivity to and respect for other cultures, active involvement in addressing issues of human and environmental sustainability.

Communication — communicate effectively orally, in writing and with a variety of digital tools; listening skills.

Critical Thinking and Problem Solving — think critically to design and manage projects, solve problems, make effective decisions using a variety of digital tools and resources.

Collaboration — work in teams, learn from and contribute to the learning of others, social networking skills, empathy in working with diverse others.

Creativity and Imagination — economic and social entrepreneurialism, considering and pursuing novel ideas, and leadership for action.

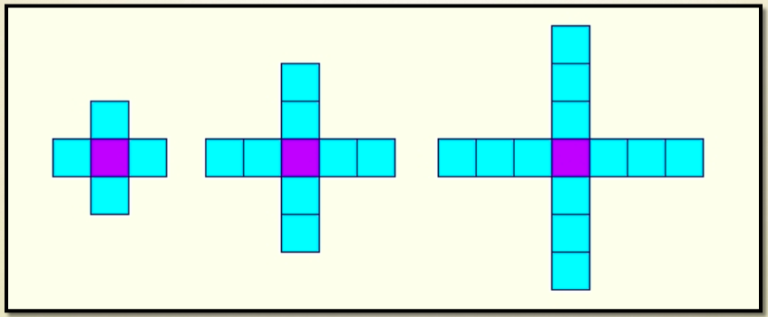
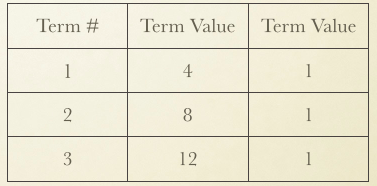
Here is an example of a growing pattern I would typically use to model the process of generating equations.

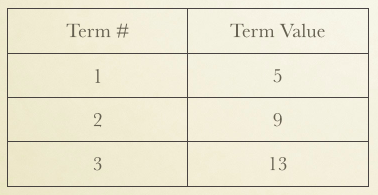
With the class we would generate a table of values.

We would also discuss the “constant” purple tile and suggest an alternative table of values.

Eventually we would determine the equation for any number of tiles in the “Nth” figure.

I would ask something along the lines of “How many tiles are there in the 7th figure?” and we would solve 4(7) + 1 = 29 tiles.

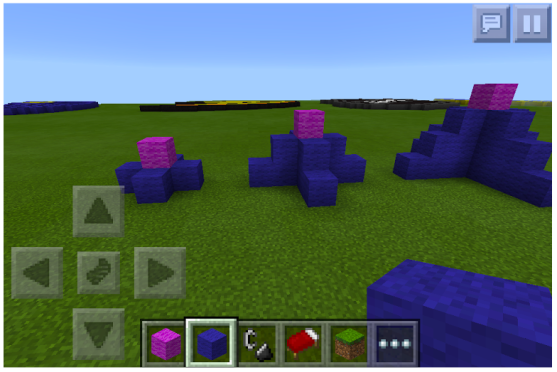
After a few examples, I would think out loud “But what if this is a top down view and the pattern is growing like a pyramid? What would it look like in 3D?” I would encourage students to brainstorm possible 3D representations of this pattern using linking cubes or Lego before introducing Minecraft.

One possible pattern might look like this.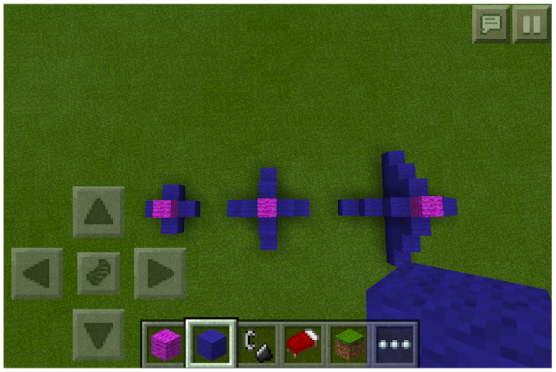

What I love about Minecraft is we now almost have an infinite number of different patterns. Minecraft allows me to personalize learning and differentiate instruction. Since it is an open “canvas” students are free to create patterns that fit their own understanding. They can push themselves and challenge each other to determine possible pattern rules.

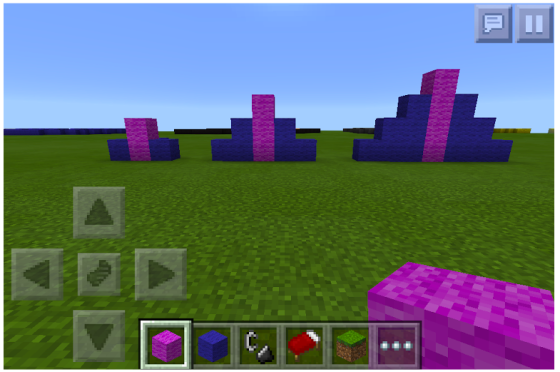
In the above example, I would ask if the purple cube was a constant “one” or if there were purple cubes inside too. This provides an example opportunity for students to explore their own spatial awareness and computational strategies.

Perhaps the inside of this pyramid looks like this. Perhaps not. Either way, the students will surely be using math vocabulary as they inquire and explore. Maybe you as the teacher can determine a set of challenges.

No iPads (or Minecraft PC account)? No problem. The above examples can be done with Lego or linking cubes.

Have iPads (or a PC version)? SWEET – Read on!

Possible Next Steps:

Perhaps you also teach Science. Here is an opportunity to do some really cool things!

From the Science curriculum:

Overall Expectations:

• design and construct a variety of structures, and investigate the relationship between the design and function of these structures and the forces that act on them;
• demonstrate an understanding of the relationship between structural forms and the forces that act on and within them.

Specific Expectations:

• classify structures as solid structures (e.g., dams), frame structures (e.g., goal posts), or shell structures (e.g., airplane wings);
• identify and describe factors that can cause a structure to fail (e.g., bad design, faulty construction, foundation failure, extraordinary loads);
• describe the role of symmetry in structures (e.g., aesthetic appeal, structural stability).

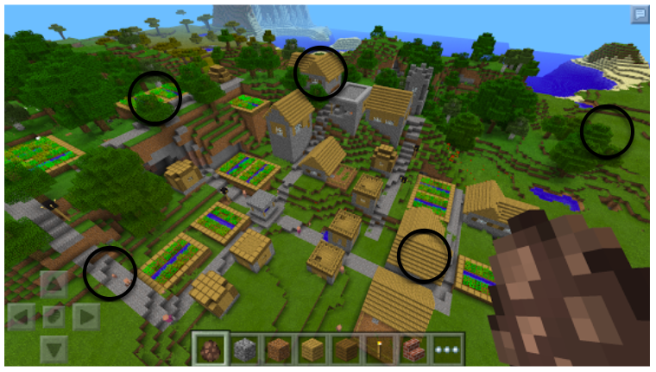
After students have grasped the basic “patterning” concepts and basic “structure” concepts, challenge them to build a “game”. Challenge them to build a world where each figure in a pattern is hidden inside different structures. The player of the game might have to solve clues to find the next figure in order to determine the pattern rule. Really rich stuff. Clues could be written to support your Literacy program. Perhaps they could write narrative stories about this world or explanations of each structure. Possibilities are only limited by your creativity!

Have students screenshot their world and map the locations of each figure as an answer key.

Everything you see here can be done with the pocket edition of Minecraft. Currently it is $7.99.

A few questions to consider:

How would you extend or alter this lesson?

How long would you work on a project like this? 

Would they work in groups?

How would you assess it?