 For all the kids who grow up in a small town and think they don’t stand a chance. You do. I was once that kid.
For all the kids who grow up in a small town and think they don’t stand a chance. You do. I was once that kid.
What is the one thing you have always wanted to try? Why haven’t you done it? Surround yourself with people who make you better and use them as your safety net. Brian cleverly articulates the importance of taking risks in order to achieve success. With the ever growing demand for problem solvers in industry, he makes incredibly valid points about our current school system and discusses potential criteria for change. In a world that changes overnight, the only strategy guaranteed to fail is not trying something new
Follow Brian’s twenty year adventure as an educator and entrepreneur. From flipping computers in high school, to flipping apps in his twenties, to flipping real estate in his thirties, you won’t want to miss this roller coaster of a ride. Brian is transparent in his own learning and shares many secrets to financial freedom through his natural storytelling, humour, and passion. There is no such thing as failure when you hustle. The secret to growth is watching the landscape and learning to pivot.
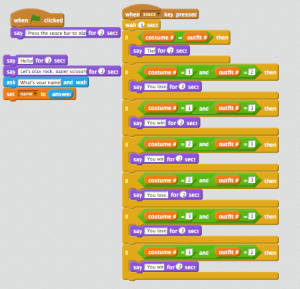

Brian, I always appreciate how you share the games that you make, and I can certainly see how this game would help with getting a larger sample size for Rock, Paper, Scissors. I’m thinking about probability though. We spend so much time in the primary grades playing probability games. Is there more to probability than games though? I remember having this conversation when I taught Grade 5, and looking at some more real world examples of probability. This definitely seemed to link more with critical thinking. What do you think? How do we balance the games and the other options? Do we provide enough of these other options? Thoughts?
Aviva
Maybe intertwine language of probability wherever it fits in classroom conversations – impossible, likely, certain…, and connect to fractional language, number value lines, relate to ‘out of 10’, ‘on a scale of 1 – 10’, majority, and of course percents and decimals as appropriate. Setting up proportional reasoning within probability will prepare for that flexible thinking we hope they develop!